
For the last 100 years or so statisticians and econometricians have spent all of their energy solving the wrong statistical problem.
In statistics we are interested in determining what happens to some outcome of interest (Y) after making a change to some other observable variable (X). For example, we are interested in increasing survival from colon cancer (Y to Y') using some new drug treatment (X to X'). The problem is there is some unobservable characteristic of the patient or the drug or both (U) that may determine both patient survival and the use of the new drug treatment.
There are two statistical problems.
The first one, the one we spend all our energy on, is called "confounding." In the picture above this problem is represented by the line running from U to X. The unobserved characteristic of the patient is determining the treatment the patient receives. In this paper, there seems to be a tendency for oxaliplatin to be given to healthier patients which may explain the survival difference between the oxaliplatin group and the non-oxaliplatin group. To solve this problem we spend millions and millions of dollars every year to run randomized control trials. In economics, we devise fancy and clever ways of overcoming the confounding with instrumental variables.
The second problem doesn't really have a name. I will call it "mediating." This problem is represented in the picture by the line from U to Y. The problem is that there may be some unobserved characteristic of the patient that is mediating the effect of the treatment on the patient's survival. Oxaliplatin may have greater effect on survival for younger patients relative to older patients (see here). We do not spend any money or much time devising ways to solve this problem. In fact, we often give up before we start by saying that it is impossible because it is not possible to observe the same patient's outcome under two different treatments.
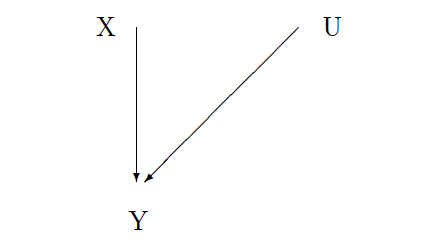
The problem with spending all our time on the first problem is that once we solve it we are still no closer to solving the second problem and we still don't know what will happen to any patient when given the treatment being studied.
In the graph to the left, the outcome (Y) is a function of both the treatment (X) and the unobserved patient characteristic (U). Although the experiment removes the line between U and X, the line between U and Y remains.
We can conduct as many experiments as we like and still be no closer to knowing what will happen when we give the treatment to a new patient because we don't know anything about that patient's unobserved characteristics.
We can conduct as many experiments as we like and still be no closer to knowing what will happen when we give the treatment to a new patient because we don't know anything about that patient's unobserved characteristics.
